Next: Naive Bayes
Up: Basic Learning Rules
Previous: Winnow
Contents
Perceptron
The Perceptron update rule is implemented similarly. It takes only two
parameters, a threshold 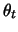 and a learning rate
and a learning rate 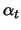 . As in
Winnow, whenever a mistake is made, the weights of active features are
updated. In this case, they are updated via either addition or subtraction,
depending on whether the mistake was made on a positive or negative example
respectively.
. As in
Winnow, whenever a mistake is made, the weights of active features are
updated. In this case, they are updated via either addition or subtraction,
depending on whether the mistake was made on a positive or negative example
respectively.
A Perceptron update proceeds as follows:
- Let
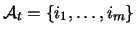 be the set of active features in a
given example that are linked to target node
be the set of active features in a
given example that are linked to target node 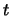 , and let
, and let 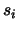 be the
strength associated with feature
be the
strength associated with feature 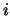 in the example.
in the example.
- If the algorithm predicts negative (that is,
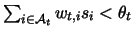 ), and the specified label is positive, the weights of
features active in the current example are promoted in an additive
fashion:
), and the specified label is positive, the weights of
features active in the current example are promoted in an additive
fashion:
- If the algorithm predicts positive (
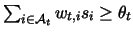 ) and the specified label is negative, the weights of features
active in the current example are demoted:
) and the specified label is negative, the weights of features
active in the current example are demoted:
- All other weights are unchanged.
Perceptron's sigmoid activation is calculated with the following formula:
This is exactly the formula used by [Mitchell, 1997] as a sigmoid function in
the context of neural networks.
Next: Naive Bayes
Up: Basic Learning Rules
Previous: Winnow
Contents
Cognitive Computations
2004-08-20