Winnow

Next: Perceptron Up: Basic Learning Rules Previous: Basic Learning Rules Contents

Winnow

The Winnow update rule has, in addition to the threshold $\theta_t$ at target node

, two update parameters: a promotion parameter $\alpha_t > 1$ and a demotion parameter $0 < \beta_t < 1$ . These are used to update the current hypothesis in

(the set of weights $w_{t,i}$ ) only when a mistake in prediction is made.

A Winnow update proceeds as follows:

Let ${\cal A}_t = \{i_1, \ldots, i_m \}$ be the set of active features in a given example that are linked to target node , and let be the strength associated with feature in the example.
If the algorithm predicts negative (that is, $\sum_{i \in {\cal A}_t} w_{t,i} s_i < \theta_t$ ), and the specified label is positive, the weights of features active in the current example are promoted in a multiplicative fashion:

$\displaystyle \forall i \in {\cal A}_t, w_{t,i} \leftarrow w_{t,i} \cdot \alpha_t^{s_i}$
If the algorithm predicts positive ( $\sum_{i \in {\cal A}_t} w_{t,i} s_i \ge \theta_t$ ) and the specified label is negative, the weights of features active in the current example are demoted:

$\displaystyle \forall i \in {\cal A}_t, w_{t,i} \leftarrow w_{t,i} \cdot \beta_t^{s_i}$
All other weights are unchanged.

In SNoW, Winnow's sigmoid activation is calculated with the following formula:

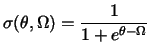
$\displaystyle \sigma(\theta, \Omega) = \frac{1}{1 + e^{\theta - \Omega}}$

where $\theta$ is a target's threshold and $\Omega$ is a target's activation with respect to an example.

The key feature of the Winnow update rule [Littlestone, 1988] is that the number of examples required to learn a linear function grows linearly with the number of relevant features and only logarithmically with the total number of features^4.6. This property seems crucial in domains in which the feature space is vast, but a relatively small number of features is relevant (this does not mean that only those will be active, or have non-zero weights). Winnow is known to learn any linear threshold function efficiently, to be robust in the presence of various kinds of noise and in cases where no linear threshold function can make perfect classification, and to still maintain its above-mentioned dependence on the number of total and relevant attributes [Littlestone, 1991,Kivinen and Warmuth, 1997].

We note that the original Winnow algorithm is a positive weight algorithm. Therefore, it is typically not expressive enough for applications. Using the ``duplication trick'' [Littlestone, 1988] is not feasible when the number of features is very large but only a small number of them is active in each example. The default SNoW architecture instantiation, using one target node for each class label (two target nodes for Boolean functions), resolves this issue. Note also that this is different from the balanced version of Winnow. This version can be run in SNoW as a special case of the true multi-class training policy (see below).

Footnotes

... features ^4.6: In the on-line setting this is usually phrased in terms of a mistake-bound but is known to imply convergence in the PAC sense [Valiant, 1984,Helmbold and Warmuth, 1995].

Next: Perceptron Up: Basic Learning Rules Previous: Basic Learning Rules Contents

Cognitive Computations 2004-08-20