Next: Threshold-Relative Updating Up: Extensions to the Basic Previous: Sequential Model Contents


Voting: The Clouds Architecture

Each target node in SNoW is learned as a linear function of the features found active with its target ID in the training set. One way to increase the expressivity of this representation is to allow each target (class label) to be represented as a weighted combination of target nodes' output. SNoW supports this by allowing more than one target node, potentially learned by different learning algorithms, to represent the same class label. Those that do are grouped into clouds, in which they collectively provide the output for a single target. For example, target $ 1$ could be the combination of two target nodes, one learned using Perceptron and one learned using Winnow, while target $ 2$ is a combination of a naive Bayes learner and a Winnow learner.

Each linear function that participates in this combination is trained individually according to its own parameters. Only at decision time is the target's prediction confidence determined as a weighted sum of the individual target nodes' sigmoid activations with coefficients that are a function of the cumulative number of mistakes made by each target node in the cloud during training. In light of this, the target $ t^*$ predicted by SNoW's winner-take-all testing policy for an example $ e$ can be stated more generally than it was in Section 4.1 as:

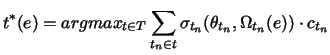
$\displaystyle t^*(e) = argmax_{t \in T} \sum_{t_n \in t} \sigma_{t_n}(\theta_{t_n}, \Omega_{t_n}(e)) \cdot c_{t_n} $

where $ T$ is the set of all possible predictions (class labels), each $ t_n$ is a target node, $ \theta_{t_n}$ is the threshold of the algorithm associated with $ t_n$, $ \Omega_{t_n}(e)$ is the activation calculated by $ t_n$ for $ e$, $ \sigma_{t_n}(\theta, \Omega(e))$ is the algorithm specific sigmoid function discussed in Sections 4.1 and 4.2, and $ c_{t_n}$ is $ t_n$'s cloud confidence (discussed next).

Cloud confidence is a floating point value stored in each target node and initialized to $ 1$. When $ t_n$ makes a mistake during training, its cloud confidence $ c^{t_n}$ is updated with the following formula:

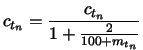
$\displaystyle c_{t_n} = \frac{c_{t_n}}{1 + \frac{2}{100 + m_{t_n}}} $

where $ m_{t_n}$ is the total number of mistakes made by target node $ t_n$ so far. This formula was designed to decrease cloud confidence at a decreasing rate so that a cloud confidence value is still representable by a double-precision floating point variable after many mistakes. Note that the value that $ c_{t_n}$ is divided by approaches $ 1$ as the number of mistakes approaches $ \infty$. For instance, after the first mistake, the cloud confidence of $ t_n$ is roughly $ 0.98$. After $ 100$ mistakes, the cloud confidence is roughly $ 0.25$, and after $ 1,000,000$ mistakes, the cloud confidence is roughly $ 1.03 \cdot 10^{-8}$.

Cloud confidence values are only updated in SNoW's -train mode. After SNoW has finished training on all examples, cloud confidences are then normalized so that they sum to 1 within each cloud. When incremental learning is enabled (see the -i option) and SNoW is in -test mode, cloud confidence values are read from the network file and used in example evaluation, but they are not updated.


Next: Threshold-Relative Updating Up: Extensions to the Basic Previous: Sequential Model Contents
Cognitive Computations 2004-08-20